Teorema de Pitot
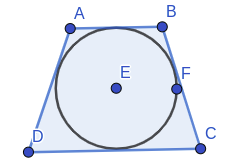
El teorema de Pitot nos dice que en un cuadrilátero convexo que inscribe una circunferencia la suma de las longitudes de los lados opuestos son iguales.
Un cuadrilátero cíclico es un cuadrilátero que se puede inscribir en una circunferencia. El teorema de Pitot establece que la suma de las longitudes de los lados opuestos de un cuadrilátero cíclico es igual a la suma de los productos de las longitudes de los diagonales opuestas.
Matemáticamente, si tenemos un cuadrilátero cíclico ABCD, donde AB, BC, CD y DA son los lados y AC y BD son las diagonales, entonces el teorema de Pitot se puede expresar de la siguiente manera:
AB + CD = BC + DA = AC + BD
Aplicaciones del teorema de Pitot
El teorema de Pitot tiene varias aplicaciones en la resolución de problemas de geometría que involucran cuadriláteros cíclicos. A continuación, se presentan algunas aplicaciones comunes:
Encontrar longitudes desconocidas
El teorema de Pitot se puede utilizar para encontrar longitudes desconocidas de un cuadrilátero cíclico. Si conocemos las longitudes de dos lados opuestos y las diagonales opuestas, podemos utilizar el teorema para encontrar las longitudes de los otros dos lados.
Encontrar ángulos desconocidos
El teorema de Pitot también se puede utilizar para encontrar ángulos desconocidos de un cuadrilátero cíclico. Si conocemos las longitudes de dos lados opuestos y las diagonales opuestas, podemos utilizar el teorema para encontrar los ángulos opuestos correspondientes.
Resolver problemas de congruencia
El teorema de Pitot también se puede utilizar para probar la congruencia entre cuadriláteros cíclicos. Si dos cuadriláteros cíclicos tienen las longitudes de los lados opuestos y diagonales opuestas iguales, entonces los cuadriláteros son congruentes.
Resolver problemas de simetría
El teorema de Pitot también se puede utilizar para probar la simetría de un cuadrilátero cíclico. Si un cuadrilátero cíclico tiene lados opuestos y diagonales opuestas iguales, entonces el cuadrilátero es simétrico respecto a su centro.